Науку, которая изучает механическое движение материальных тел и их взаимодействие, которое при этом происходит, называют механикой. В зависимости от описания движения в механике выделяют разделы: кинематику, где изучается движение тел, не считая силы; динамику, которая изучает движение тел под действием сил; статику, которая изучает вопрос равновесия тел.
Виды механического движения
Однако не все движения можно описать законами механики. Например, движение одной молекулы можно описать законами механического движения, а движение их совокупности в веществе описывается уже другими — статистическими законами. Движение тела со скоростью, близкой к скорости света,
описывается законами релятивистской механики. Движение и взаимодействие элементарных частиц микромира описывают в квантовой механике.
Законы механического движения, которые мы будем изучать в этой статье, распространяются на тела макро- и мегамиров, движущихся со скоростями, намного меньшими скорости света. Механические движения тел могут быть разнообразными и сложными. На рисунке ниже показаны примеры поступательного, вращательного и колебательного движений.
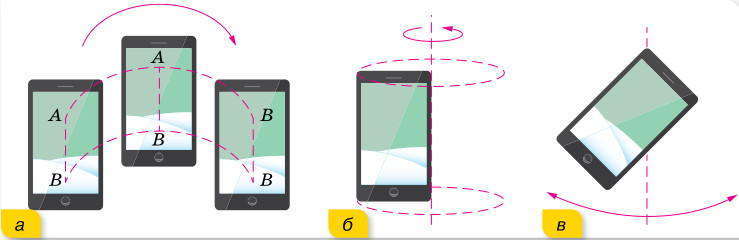
б — вращательное, в — колебательное
В природе, как правило, тела одновременно осуществляют несколько движений. Например, Земля вращается вокруг собственной оси, вокруг Солнца, и вместе с Солнцем движется по направлению к звезде Вега.
Обратите внимание, в этом случае мы Землю рассматривали как материальную точку. Так можно идеализировать движение, если размеры и форма тела в рассматриваемом движении не существенные и ими можно пренебречь. В дальнейшем, если нет специальных оговорок, употребляя слово тело, следует иметь в виду, что его можно рассматривать как материальную точку.
Основная задача механики
Основной задачей механики является описание механического движения тел, то есть установление закона движения (уравнения движения) тела на основе его характеристик (координат, перемещения, длины пройденного пути, угла поворота, скорости, ускорения и т.д.). Иными словами, если с помощью составленного закона (уравнения) движения можно определить положение тела в любой момент времени, то основная задача механики считается решенной.
Итак, основной задачей механики является определение положения тела в пространстве в любой момент времени. Рассмотрим способы определения положения тела. Чтобы фиксировать изменение положения тела в пространстве, необходимо установить, относительно чего происходит именно это изменение. Систему отсчета в кинематике выбирают, руководствуясь лишь соображениями удобства для математического описания движения.
Уравнение, устанавливающее зависимость координат материальной точки от времени, называется уравнением (законом) движения. В трехмерной системе отсчета уравнения движения математически записывают так: х = x (t), у = y (t), z = z (t).
Исследовать движение тела (изменение его положения в пространстве с течением времени) можно и по его траектории. Траектория материальной точки — непрерывная воображаемая линия, которую описывает точка во время своего движения в выбранной системе отсчета.
По траектории движения легко определить путь, пройденный телом. Для этого необходимо измерить длину траектории между начальным положением тела и положением тела в выбранный момент времени.
Путь, l — физическая величина, равная длине траектории, которую описывает точка при движении. Единицей пути является метр: 1 м. Путь — величина скалярная.
Если известно, где находится тело в начале движения, его траектория и пройденный путь, то можно определить, где будет тело в конце движения.
Если траектория движения неизвестна, и не имеет значения, по какой именно траектории движется тело, а важно определить изменение положения тела в пространстве с течением времени, тогда пользуются понятиями «радиус-вектор» и «перемещение».
Радиус-вектор r точки — это вектор, соединяющий начало отсчета с этой точкой. 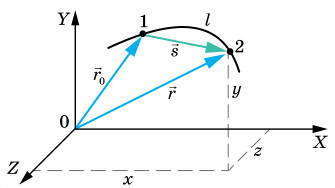 Например, в начальный момент времени тело находится в точке 1 (рисунок справа), положение которой определяется радиусом-вектором ro. В течение интервала времени ∆t тело переместилось в точку 2, положение которой определяется радиусом-вектором r. Изменение положения тела можно определить по его перемещениям.
Например, в начальный момент времени тело находится в точке 1 (рисунок справа), положение которой определяется радиусом-вектором ro. В течение интервала времени ∆t тело переместилось в точку 2, положение которой определяется радиусом-вектором r. Изменение положения тела можно определить по его перемещениям.
Перемещение s — вектор, соединяющий начальное положение точки с ее положением в выбранный момент времени. Как видно из рисунка, вектор перемещения s, проведенный из начальной точки 1 в конечную 2, равен приросту радиус-вектора:
![]()
Модуль вектора перемещения обозначают |s|, или просто s. Единицей перемещения является метр: 1 м.
Векторная величина (вектор) — величина, значение которой задается действительным числом и направлением. Графически вектор изображают направленным отрезком, чем задают сразу три характеристики: числовое значение, направление и точку приложения.
Проекция вектора на ось — это длина отрезка, который получают благодаря проектированию вектора на соответствующую координатную ось.
В декартовой системе координат, чтобы спроектировать вектор, надо опустить перпендикуляры на оси из точек начала и конца вектора. Проекцией вектора а на ось X называется величина ах, равная ax = a*cosϕ, где а — модуль вектора, ϕ — угол между направлением вектора и осью X.
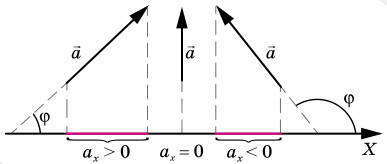
Проекция вектора на ось будет положительной, если угол ϕ острый, и отрицательной, если угол ϕ тупой, и равна нулю, если ϕ прямой (вектор перпендикулярен к оси).
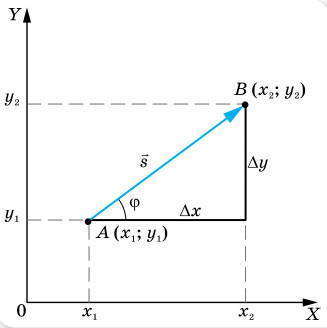
Вектор перемещения тела можно определить по его координатам. Пусть тело находится на плоскости в точке 1, координаты которой х1 и y1. За определенный интервал времени тело переместилось в точку 2, координаты которой х2 и у2. Из рисунка видно, что модуль и направление вектора перемещения s могут быть определены через разности координат ∆x = x2 – x1 и ∆y = y2 – y1 .
Модуль вектора перемещения ![]() или
или ![]() .
.
Направление вектора перемещения относительно координатной оси X определяется тангенсом угла наклона вектора:
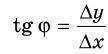
И наоборот, разница координат может быть выражена через модуль вектора перемещения:
![]()
Таким образом, определить положение движущегося тела относительно выбранной системы отсчета можно тремя способами: координатным, векторным и траекторных (естественным). Координатным способом положение движущегося тела в пространстве можно определить, если известен закон изменения координат со временем:
x = x(t), y = y(t), z = z(t)
Векторным способом положения движущегося тела в пространстве можно определить по его радиусу-вектору r(t). Траекторных (естественным) способом положения тела определяется по пройденному пути вдоль траектории l = l(t). Этот способ применим, когда траектория движения известна.
Иногда можно записать формулу, которая связывает координаты точки при движении на плоскости — зависимость х = f(y). Эта формула называется уравнением траектории. Отметим, что можно рассматривать движение не только между начальным и конечным положениями тела, но и в любой момент времени его движения.
