Электроемкость проводников различной формы
Мы уже узнали, что в проводнике, помещенном в электрическое поле, происходит перераспределение зарядов до тех пор, пока внешнее поле внутри проводника не скомпенсируется собственным полем разделенных зарядов. Все заряды размещаются на внешней поверхности проводника, которая является эквипотенциальной. Потенциал любой точки этой поверхности считается потенциалом всего проводника.
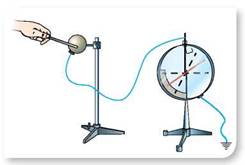
Выясним, как будет меняться потенциал проводника при изменении его заряда. Возьмем проводник (например, металлический шар), изолированный от земли и других проводников, и, не меняя его положение относительно других проводников, будем его электризовать (увеличивать заряд). С помощью электрометра можно измерять соответствующие значения потенциала проводника. Во сколько раз увеличивается заряд шара, во столько же возрастает его потенциал, то есть заряд проводника прямо пропорционален потенциалу, q ~ φ. Вводя коэффициент пропорциональности, получаем q = Cφ, где С — коэффициент пропорциональности, постоянный для условий данного опыта. Если мы заменим проводник другим (например, шаром больших размеров) или изменим внешние условия опыта, то значение коэффициента С будет другим. Этот коэффициент пропорциональности называют емкостью (или электроемкость) проводника.
Электрометр, или электростатический вольтметр — прибор для измерения потенциала заряженного проводника относительно Земли или в отношении другого заряженного проводника.
Электроемкость С — скалярная физическая величина, характеризующая способность проводников накапливать и удерживать определенный электрический заряд. Она измеряется отношением заряда q, который предоставили изолированному проводнику, к его потенциалу φ,
![]()
Единица электроемкости — фарад, 1 Ф.
Электроемкость проводника правильной формы можно рассчитать. Например, вычислим емкость отдельной ведущей шара радиусом r. Потенциал заряженного шара
![]()
подставляя это выражение в формулу для емкости, получаем: C = 4πε0εr.
Следует отметить, что емкость 1 Ф очень большая. Так, с помощью последней формулы можно показать, что в вакууме электроемкость в 1 Ф имеет шар радиусом 9 · 109 м (что в 23 раза больше расстояния от Земли до Луны). Емкость Земли, радиус которой 6,4 · 106 м, равна 7 · 10 -4 Ф.
Поэтому на практике чаще всего используют микро- и пикофарадами: 1 мкФ = 10-6 Ф, 1 пФ = 10-12 Ф.
Опыты показывают, что емкость проводника зависит от его размеров и формы. Однако она не зависит от материала, агрегатного состояния, формы и размеров полости внутри проводника (объясните самостоятельно почему). Выясним условия, от которых зависит электроемкость проводника.
Поскольку проводник электризуется через внешнее влияние, электроемкость проводника должно зависеть от размещения вблизи него других проводников и от окружающей среды. Покажем это на опыте. Возьмем два металлические диски, закрепленные на подставках из диэлектрика. Диск А соединим с электрометром, корпус которого заземлен, а диск В отодвинем от диска А. наэлектризует диск А, предоставив ему заряд, который в дальнейшем не будет меняться. Определив значение потенциала диска А по показаниям электрометра, начнем приближать к нему диск В, одновременно наблюдая за стрелкой прибора. Оказывается, что потенциал диска А при этом уменьшается.
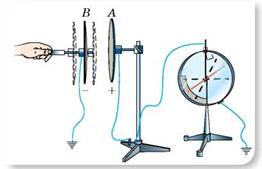
Еще резче уменьшение потенциала диска А можно наблюдать, если заземлить диск В. Принимая во внимание, что заряд на диске А при этом не меняется, делаем вывод, что уменьшение потенциала обусловлено увеличением электроемкости системы дисков. Заменив воздух между дисками другим диэлектриком, снова заметим увеличение электроемкости системы дисков.
Заземление предметов — это соединение их с землей (проводником) с помощью металлических листов, закопанных в землю, водопроводных труб и тому подобное.
Результаты опытов можно объяснить так. Когда диск В попадает в поле диска А, он электризуется и создает свое поле. Если соединить диск В с землей, на нем останутся только заряды противоположного знака по сравнению с зарядами на диске А. Это усиливает поле диска В, которое еще больше уменьшает потенциал диска А. Если внести между диски диэлектрик, то он поляризуется. Поляризационные заряды, расположенные вблизи поверхности диска А, компенсируют часть его заряда, следовательно, электроемкость диска возрастает.
Конденсатор. Электроемкость плоского конденсатора.
Рассмотренная система проводников является основой для устройств, которые называют конденсаторами. Конденсаторы широко используют в радиотехнике как устройства для накопления и удержания электрического заряда.
Самый простой конденсатор состоит из двух или более разноименно заряженных и разделенных диэлектриком проводников, которые называют обкладками конденсатора. Последние имеют одинаковые по абсолютному значению разноименные заряды и размещены относительно друг друга так, что поле в этой системе сконцентрировано в ограниченном пространстве между обкладками. Диэлектрик между обкладками играет двойную роль: во-первых, он увеличивает электроемкость, во-вторых — не дает зарядам нейтрализоваться. Поэтому диэлектрическая проницаемость и электрическая прочность на пробой (пробой диэлектрика означает, что он становится проводником) должны быть достаточно большими. Чтобы защитить конденсатор от механических внешних воздействий, его помещают в корпус.
Накопление зарядов на обкладках конденсатора называют его зарядкой. Чтобы зарядить конденсатор, его обкладки присоединяют к полюсам источника напряжения, например, к полюсам батареи аккумуляторов. Можно также соединить одну обкладку с полюсом батареи, второй полюс которой заземлен, а вторую обкладку конденсатора тоже заземлить. Тогда на заземленной обкладке останется заряд, противоположный по знаку, а по модулю он будет равен заряду другой обкладки. Такой же по модулю заряд уйдет в землю.
Под зарядом конденсатора понимают абсолютное значение заряда одной из обкладок. Он прямо пропорционален разности потенциалов (напряжению) между обкладками конденсатора. В таком случае емкость конденсатора (в отличие от отдельного проводника) определяется по формуле
![]()
По форме обкладок конденсаторы бывают плоские, цилиндрические и сферические. Как диэлектрик в них используют парафиновый бумагу, слюду, воздух, пластмассы, керамику и тому подобное. Типичный плоский конденсатор состоит из двух металлических пластин площадью S, пространство между которыми разделено диэлектриком толщиной d.
Выведем формулу для емкости плоского конденсатора. Учитывая, что
![]()
подставим в эту формулу выражение U = Ed, где Е — напряженность поля, создаваемого двумя пластинами,
![]()
В результате получим:
![]()
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади перекрытия пластин и относительной диэлектрической проницаемости диэлектрика и обратно пропорциональна расстоянию между пластинами. Из формулы следует, что, уменьшая толщину диэлектрика между пластинами или увеличивая площадь перекрытия пластин, можно получить конденсатор большей емкости.
Соответственно можно вывести формулы для емкости конденсаторов других форм. Так, емкость сферического конденсатора вычисляется по формуле
![]()
где r и R- радиус внутренней и внешней сфер (в случае обособленной шара, когда R = ∞, имеем: C = 4пε 0 εr).
Соединение конденсаторов
Во многих случаях, чтобы создать нужную электроемкость, конденсаторы соединяют в группу, которая называется батареей.
Последовательным называют такое соединение конденсаторов, при котором отрицательно заряженная обкладка предварительного конденсатора соединена с положительно заряженной обкладкой следующего. В случае последовательного соединения на всех обкладках конденсаторов будут одинаковые по модулю заряды, соответственно одинаковыми будут и потенциалы обкладок, соединенных между собой проводниками.
Учтя это, выведем формулу для вычисления электроемкости батареи последовательно соединенных конденсаторов. Напряжение на батарее U бы равна сумме напряжений на последовательно соединенных конденсаторах, действительно (φ 1 — φ 2 ) + (φ 2 — φ 3 ) + … + (φ n -1 — φ n ) = φ 1 — φ n или U 1 + U 2 + … + U n = U бы . Использовав соотношение q = CU, получим
![]()
Сократив на q, получим
![]()
Следовательно, для последовательного соединение электроемкость батареи меньше наименьшей из электроемкости отдельных конденсаторов.
Параллельным называется соединение конденсаторов, при котором все положительно заряженные обкладки присоединены к одному проводнику, а отрицательно заряженные — к другому. В этом случае напряжения на всех конденсаторах одинаковы и равны U, а заряд на батареи равна сумме зарядов на отдельных конденсаторах, q б = q 1 + q 2 + … + q n , откуда C бы U = C 1 U + C 2 U + … + C n U. После сокращения получаем формулу для вычисления электроемкости батареи параллельно соединенных конденсаторов, С б = C 1 + C 2 + … + C n. Для параллельного соединения электроемкость батареи больше, чем самая большая из электроемкости отдельных конденсаторов (равна сумме емкостей всех конденсаторов).
Энергия заряженного конденсатора. Как и любая система заряженных тел, конденсатор обладает энергией. Для того чтобы зарядить конденсатор, нужно выполнить работу, затрачиваемое на разделение положительных и отрицательных зарядов. Согласно закону сохранения энергии, эта работа равна энергии конденсатора A = W эл .
Как известно, работа сил электрического поля по перемещению заряда на определенное расстояние равно A = qU, если напряжение постоянное (U = const). В случае подзарядки конденсатора напряжение на его обкладках растет от нуля до U, и, вычисляя работу поля, в этом случае нужно использовать ее среднее значение
![]()
соответственно энергия заряженного конденсатора
![]()
Поскольку q = CU, то получим еще две формулы для вычисления энергии конденсатора:
![]()
