Поток напряженности электрического поля. Теорема Остроградского — Гаусса.
Рассмотрим поле точечного положительного заряда. Количество силовых линий N можно изобразить произвольно, поскольку поле существует во всех точках пространства вокруг заряда. Окружим мысленно заряд сферами, центр которых совпадает с точечным зарядом. Как видно, количество линий напряженности, которые пересекают первую и вторую сферы, одинакова. Какую бы количество сфер мы не построили, количество линий напряженности, которые их пересекают остается одинаковой. Иллюстрация к введению понятия потока напряженности электрического поля:

Модуль напряженности поля, создаваемого точечным зарядом q, в произвольной точке сферы радиусом r составляет:
![]()
перепишем эту формулу в таком виде:
![]()
Площадь сферы S = 4пr 2 , следовательно, данная формула приобретает вид:
![]()
Поскольку площадь сферы увеличивается, как квадрат радиуса, а напряженность поля в точках на сфере уменьшается, как квадрат радиуса, произведение ES остается одинаковым для всех сфер.
Ранее мы установили, что одинаковой для всех сфер будет количество линий напряженности, которые их пересекают, N. Итак, с точностью до некоторой постоянной можно приравнять: ES = N или
![]()
Как видно из последней формулы, количество линий напряженности, выходящих из точечного заряда, пропорциональна величине этого заряда.
В рассматриваемом случае поверхность сферы площадью S, внутри которой содержится точечный заряд, является замкнутой поверхностью, перпендикулярной к линиям напряженности. Для этого случая мы и получили:
![]()
Такой же результат можно получить и для произвольной системы зарядов: если окружить произвольную систему зарядов замкнутой поверхностью (не обязательно сферой), то количество силовых линий, пересекающих эту поверхность, определяется суммарным зарядом системы,
![]()
Это утверждение называют теоремой Остроградского — Гаусса.
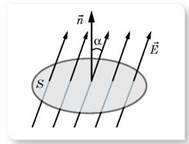
Совокупность линий напряженности, которые пересекают плоскость, перпендикулярную к линиям напряженности и площадь которой S, называют потоком вектора напряженности, N = ES.
Если поверхность не перпендикулярна направлению вектора напряженности электрического поля, то формула записывается так: N = ES cos α, где α — угол между направлением вектора напряженности E и нормали к поверхности.
Теорема Остроградского — Гаусса формулируют так:
Поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен
![]()
где Σqi — алгебраическая сумма зарядов, находящихся внутри этой поверхности.
Примеры применения теоремы Остроградского — Гаусса.
Теорема Остроградского — Гаусса облегчает нахождение значений вектора Е, когда площадь поверхности охватывает заряд, легко вычислить по формулам геометрии. Например, вычислим напряженность поля, создаваемого равномерно заряженной сферой. Но перед этим введем понятие плотности электрического заряда.
Плотность электрического заряда — физическая величина, характеризующая распределение электрического заряда в пространстве.
Также пользуются понятиями:
• линейной плотности τ, если электрический заряд q распределен вдоль линии длиной l,
![]()
• поверхностной плотности σ, если заряд q распределен по поверхности площадью S,
![]()
• объемной плотности ρ, если электрический заряд q распределен по всему объему V,
![]()
Если на поверхности сферы радиусом R равномерно распределены заряд q, то поверхностная плотность заряда равна:
![]()
Электрическое поле заряженной сферы:
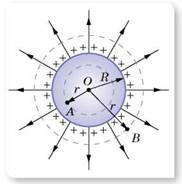
Рассмотрим внутри сферы любую точку А на расстоянии r от ее центра, то есть точку, для которой r <R. Из центра О проведем вспомогательную поверхность, тоже в виде сферы радиусом r, и вычислим поток линий напряженности N сквозь эту поверхность,
![]()
Поскольку внутри вспомогательной поверхности радиуса r электрических зарядов нет, q = 0, то и напряженность поля
![]()
также равна нулю.
Итак, внутри заряженной ведущей сферы (или другого проводника любой формы, на котором электрический заряд всегда размещается только на поверхности) электрического поля нет.
Вычислим напряженность для точек, которые содержатся у самой поверхности сферы, то есть для которых можно считать, что r = R. Тогда
![]()
Поскольку q = 4пR2σ, то
![]()
при условии, что r = R.
Для точек, которые значительно удалены от поверхности заряженной сферы (точка В на рисунке), имеем:
![]()
С помощью теоремы Остроградского — Гаусса можно вычислить напряженность электрического поля произвольных заряженных тел.
