Звездная величина или видимая яркость звезд, как мы их видим с земли, зависит от двух причин: их действительной яркости или количества света, которое они испускают, и от расстояния до нас. Если бы все звезды были одинаковой яркости, мы могли бы определять их относительное расстояние, попросту измеряя относительное количество света, получаемое от них. Количество света меняется обратно пропорционально квадрату расстояния. Это видно на прилагаемом рисунке, где S изображает положение звезды, как светящейся точки, а А и ВВВВ изображают экраны, помещенные так, что каждый из них получает одно и то же количество света от звезды.
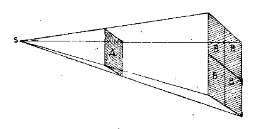
Если больший экран в два раза дальше, чем экран А, его стороны должны быть в два раза длиннее, чтобы он мог получить все то количество света, которое падает на А. Тогда его поверхность будет в 4 раза больше, чем поверхность А. Отсюда понятно, что каждая четвертая часть поверхности получит четвертую часть света, падающего на А. Таким образом глаз или телескоп, находящийся в В, получит от звезды одну четвертую часть света, сравнительно с глазом или телескопом в А, и звезда будет казаться в четыре раза слабее.
На самом деле звезды далеко не равны по их действительной яркости, а поэтому и видимая величина звезды не дает точного указания на ее расстояние. Среди более близких к нам звезд многие весьма слабы, многие даже невидимы невооруженным глазом, между тем как среди более ярких встречаются звезды, расстояния которых до вас громадны. Замечательный пример в этом отношении представляет Канолус, 2-я звезда по яркости на всем небе.
По этим причинам астрономы вынуждены ограничиться на первый случай определением количества света, которое посылают к нам различные звезды, или их видимого блеска, не принимая во внимание их расстояния или действительную яркость. Древние астрономы разделили все звезды, которые можно видеть, на 6 классов: номер класса, выражающий собою видимую яркость, называется величиной звезды. Самые яркие, в числе около 14, называются звездами первой величины. Следующие по яркости, примерно 50, называются звездами второй величины. В 3 раза больше звезд третьей величины. Примерно в такой же прогрессии увеличивается число звезд каждой величины до шестой, которая заключает в себе звезды на границе видимости.
Звезды встречаются всех возможных степеней яркости, а потому нельзя провести четкой границы между соседними величинами звезд. Два наблюдателя могут сделать две различные оценки; один причислит звезду ко второй величине, а другой к первой; некоторые звезды одним наблюдателем будут отнесены к 3-ей величине, те самые, которые для другого наблюдателя покажутся звездами второй величины. Невозможно, таким образом, с абсолютной точностью распределить звезды между отдельными величинами.
Что такое звездная величина
Понятие о величинах звезд может быть легко получено каждым случайным созерцателем небес. В любой ясный вечер видны несколько звезд 1-ой величины. Примерами звезд 2-ой величины могут служить 6 наиболее ярких звезд Ковша (Большая Медведица), Полярная Звезда, яркие звезды Кассиопеи. Все эти звезды можно видеть под нашими широтами каждую ночь в течение целого года. Звезд 3-ей величины так много, что трудно выбрать для них примеры. Наиболее яркие звезды в Плеядах именно этой величины. Впрочем, их окружают 5 других звезд, что влияет на оценку их яркости. На расстоянии 15 градусов от Полярной Звезды находится Бета Малой Медведицы: она всегда видна и отличается от Полярной Звезды красноватым оттенком; она находится между двумя другими звездами, из которых одна — 3-ей величины, а другая — 4-ой.
Пять ясно-видимых более слабых звезд Плеяд тоже все около 4-ой величины, пятой величины звезды еще свободно видимы невооруженным глазом; 6-я величина заключает в себе звезды, едва заметные для хорошего зрения.
Современные астрономы, принимая в общих чертах систему, которая дошла до них от древности, постарались придать ей большую определенность. Тщательные исследования показали, что действительное количество света, соответствующее различным величинам, меняется от одной величины до другой почти в геометрической прогрессии; это заключение согласуется с хорошо известным психологическим законом, что ощущение меняется в арифметической прогрессии, если причина, производящая его, меняется в прогрессия геометрической.
Найдено, что средняя звезда 5-ой величины дает от 2 до 3 раз больше света, чем средняя звезда 6-ой величины, звезда 4-ой величины дает от 2 до 3 раз больше света, чем звезда 5-й, и т. д., до 2-ой величины. Для первой величины различие так велико, что едва ли можно указать какое-либо среднее отношение. Сириус, например, в 6 раз ярче, чем Альтаир, который обыкновенно считается типичной звездой первой величины. Чтобы придать точность своим оценкам, современные астрономы постарались свести разницы между различными величинами к одной и той же мерке, а именно приняли, что отношение яркости звезд двух последовательных классов равно двум с половиной.
Если бы прием деления видимых звезд только на 6 отдельных величин был принят без всяких изменений, то мы бы встретили затруднение в том, что в один и тот же класс пришлось бы отнести звезды, весьма различные по яркости. В одном и том же классе оказались бы звезды, превосходящие одна другую в два раза по яркости. Поэтому, чтобы придать результатам точность, пришлось рассматривать класс, величину звезд, как такое количество, которое меняется непрерывно — ввести десятые и даже сотые доли величины. Так, мы имеем звезды 5,0, 5,1, 5,2 величины и т. д., или даже мы можем делить еще мельче и говорить о звездах, имеющих величины 5,11, 5,12 и т. д.
Измерение звездной величины
К сожалению, пока еще неизвестно никакого другого способа определять количество света, полученного от звезды, как судя по действию его на глаз. Две звезды считаются равными, когда они для глаза кажутся равной яркости. В этих условиях наше суждение весьма ненадежно. Потому наблюдатели старались придать больше точности, пуская в ход фотометры — инструменты для измерения количества света. Но даже при этих инструментах наблюдатель должен основываться на оценке глазом равенства блеска. Свет одной звезды увеличивается или уменьшается в определенной пропорции до тех пор. пока для нашего глаза он не покажется равным свету другой звезды; а эта последняя может быть и искусственной звездочкой, полученной при помощи пламени свечи или лампы. Степень увеличения или уменьшения определит разницу величин обоих звезд.
Когда мы стараемся прочно обосновать измерения блеска звезды, мы приходим к выводу, что эта задача довольно сложна. Прежде всего не все лучи, приходящие от звезды, воспринимаются нами, как свет. Но все лучи, видимые и невидимые, поглощаются черной поверхностью и выражают свое действие в нагревании ее. Поэтому самый лучший способ измерять излучение звезды состоит в оценке тепла, которое она посылает, так как это точнее отражает процессы, происходящее на светиле, чем это может сделать видимый свет. К несчастью, тепловое действие лучей звезды настолько мало, что не может быть измерено даже современными приборами. Пока что мы должны оставить надежду определить полное лучеиспускание звезды и ограничиться только той его частью, которая называется светом.
Следовательно, если мы стремимся к точности, то мы должны сказать, что свет, как мы его понимаем, может, в сущности, измеряться лишь по своему действию на зрительный нерв, и нет другого пути измерить его эффект, кроме оценки глазом. Все фотометры, которые служат для измерения света звезд, построены так, что дают возможность увеличивать или уменьшать свет одной звезды и визуально приравнивать ее к свету другой звезды или другого источника и только так оценивать ее.
Звездная величина и спектр
Трудность получения точных результатов увеличивается еще тем, что звезды различаются по их цвету. С гораздо большой точностью мы можем убеждаться в равенстве двух источников света, когда они имеют один и тот же цветовой оттенок, чем когда цвета их различны. Еще один источник неопределенности происходит от того, что называется явлением Пуркинье (Purkinje), по имени физика, который первый описал его. Он нашел, что если мы имеем два источника светя одной и той же яркости, но один красный, а другой зеленый, то при увеличении или уменьшении в одной и той же пропорции эти источники перестанут казаться одинаковыми по яркости. Другими словами, математическая аксиома о том, что половины или четверти равных величин тоже равны между собой, неприменима к действию света на глаз. Когда яркость уменьшается, зеленое пятно начинает казаться ярче, чем красное. Если мы увеличиваем яркость обоих источников, то красный начинает казаться ярче зеленого. Иначе говоря, красные лучи для нашего зрения быстрее усиливаются и ослабляются, чем лучи зеленые, при одном и том же изменении действительной яркости.
Также выяснено, что этот закон изменения кажущейся яркости не распространяется последовательно на все цвета спектра. Верно, что когда мы переходим от красного к фиолетовому концу спектра, желтый цвет гаснет менее быстро, чем красный, при данном уменьшении яркости, а зеленый — еще менее быстро, чем желтый. Но если мы переходим от зеленого к синему, то уже можно сказать, что последний не пропадает так быстро, как зеленый. Очевидно, из всего этого следует, что две звезды различного цвета, кажущиеся одинаково яркими для невооруженного глаза, уже не будут казаться равными в телескоп. Красные или желтые звезды кажутся сравнительно ярче в телескопе, зеленые и синеватые — сравнительно ярче для невооруженного глаза.
Таким образом можно сделать вывод, что, несмотря на значительное совершенствование средств измерения, развитие микроэлектроники и компьютеров, визуальные наблюдения все еще играют самую важную роль в астрономии, и вряд ли эта роль снизится в обозримом будущем.
