Так знаменитый немецкий математик Карл Вейерштрасс называл задачу о вращении твердого тела (читайте статью «Твёрдые тела, жидкости и газы«) вокруг одной неподвижной точки и отговаривал свою ученицу Софью Васильевну Ковалевскую (1850—1891) заниматься ею. Однако «самая умная и обаятельная женщина Европы» (по словам Ф. Нансена) не послушалась своего старого учителя и занялась этой, по ее словам, «дьявольской головоломкой». Но расскажем все по порядку.
В 1727 г., в год смерти Ньютона, в Петербургской Академии наук появился двадцатилетний Леонард Эйлер.
Швейцарец, выпускник университета в Базеле, он связал свою судьбу с Россией, прожил в Петербурге свои лучшие годы и там, на Смоленском кладбище, был похоронен. В Петербурге расцвел и возмужал гений Эйлера, гений, обогативший математику и механику множеством фундаментальных открытий, носящих его имя. Среди оставленных потомству 850 научных работ Эйлера жемчужиной сверкает учение о вращении тела вокруг одной неподвижной точки. Использовав ньютоновскую абсолютную и введя в рассмотрение подвижную (связанную с вращающимся телом) системы прямоугольных координат и углы рассогласования между их осями (углы Эйлера), Эйлер составил общие математические уравнения (уравнения Эйлера), характеризующие движение твердого тела вокруг одной неподвижной точки. Эти уравнения являются исходными для изучения всех возможных случаев движения твердого тела вокруг неподвижной точки. Общие уравнения сложны, решить их непросто. Сам Эйлер в 1758 г. нашел решение своих уравнений лишь для частного случая, когда центр масс тела совпадает с неподвижной точкой, а момент всех сил, приложенных к телу, равен нулю. Оказалось, что вращающееся тело, удовлетворяющее этим условиям, обладает замечательным свойством: одна из его осей, а именно та, по которой направлен вектор момента количества движения, сохраняет неизменным свое направление относительно абсолютного пространства. В большинстве технических устройств, использующих быстровращающиеся тела, направления векторов момента количества движения и угловой скорости собственного вращения тела отличается лишь на очень малые углы.
Однако направление вектора момента количества движения обычно не имеет материального воплощения, а направление вектора угловой скорости собственного вращения тела имеет, например, в виде вала маховика.
Если в целях наглядности дальнейшего изложения пренебречь малыми углами (что обычно делается на практике), то можно считать, что именно продольная ось вала маховика сохраняет неизменное направление в абсолютном пространстве. Нужно помнить, что планета Земля движется относительно абсолютного пространства. Следовательно, вращающееся тело, удовлетворяющее условиям Эйлера, сохраняя неизменное положение оси своего вращения относительно абсолютного пространства, относительно поверхности Земли будет иметь кажущееся движение.
Через 30 лет после Эйлера, в 1788 г., выдающийся французский ученый-механик Ж. Лагранж (1736—1813) нашел решение уравнений Эйлера еще для одного частного случая движения тела вокруг неподвижной точки.
Условия, накладываемые на вращающееся тело в случае, рассматриваемом Лагранжем, были менее жесткими, чем в случае Эйлера: тело предполагалось симметричным относительно оси собственного вращения, центр масс тела лежал на этой оси, но не совпадал с неподвижной точкой, движение тела рассматривалось в поле сил равномерного тяготения (классический волчок). В этом случае ось собственного вращения тела уже не сохраняла неизменным свое положение в абсолютном пространстве, а совершала сложное движение. После Эйлера и Лагранжа исследование проблемы вращения тела вокруг неподвижной точки ввиду исключительной сложности длительное время не получало дальнейшего развития. Проблема имела не только теоретическое, но и важное практическое значение. Ее более полного решения ждали астрономы, изучавшие движение громадных волчков-планет, оружейники, давно заметившие, что пули и снаряды точнее попадают в цель, если придать им, кроме поступательного, еще и вращательное движение, моряки и техники, пытавшиеся использовать замечательные свойства волчка для определения курса и получения горизонтальных площадок на качающихся палубах кораблей, а также люди многих других специальностей.
Ввиду важности проблемы французская академия наук назначила премии за какое-либо существенное продвижение в решении этой задачи. Два проведенных конкурса не дали результатов. В 1888 г. конкурс был объявлен в третий раз. Из пятнадцати представленных работ премию получила работа русского математика, профессора Стокгольмского университета Софьи Васильевны Ковалевской. Конкурсная комиссия, в состав которой входили крупнейшие ученые, высоко оценила работу С. В. Ковалевской, дав о ней лестный отзыв и увеличив премию с 3000 до 5000 франков.
Случай, рассмотренный Ковалевской, учитывал тот широко распространенный на практике факт, что центр масс вращающегося тела не лежит на оси собственного вращения и на тело действует сила тяжести.
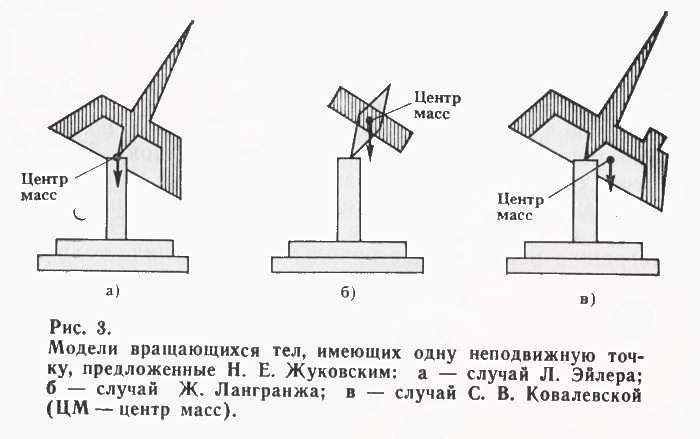В 1896 г. Н. Е. Жуковский построил на примере волчков наглядные модели для всех трех решенных в конечном виде случаев вращения твердого тела вокруг неподвижной точки. На рис. 3 представлены модели Н. Е. Жуковского. Работы Ковалевской стали исходным пунктом многочисленных исследований русских и зарубежных ученых по теории вращения твердого тела.