Предпосылки создания современной модели атома
Слово атом в буквальном переводе означает «неделимый». Впервые этим термином воспользовался древнегреческий ученый Демокрит (300 гг. до н.э.), который считал атомы мельчайшими материальными частицами, не поддающиеся внешнему воздействию и никогда не меняющиеся. Такие метафизические представления о структуре атома господствовали в химии до конца ХIX в., когда благодаря большому количеству выдающихся открытий стало понятно, что атом — это очень сложная система.
Среди важных исследований необходимо вспомнить опыты Фарадея (XIX в.) по изучению процессов, происходящих при пропускании электрического тока через жидкости, открытие Круксом невидимых катодных лучей в вакууме, которые вызывает флюоресценцию (свечение) стекла вокруг анода, а также изучение фотоэффекта — явления, которое возникает при излучении электронов в результате прокаливания или ультрафиолетового облучения металлов. На базе этих исследований Крукс (1880 г.) высказал гипотезу о отрицательно заряженных частицах, которые Томсон предложил назвать электронами (1897 г.).
Электрон — это элементарная частица, которая имеет наименьший из существующих в природе отрицательных электрических зарядов (величиной 1,60 × 1 -19 Кл) и массу 9,1095 · 10 -28 г, которая примерно в 1840 раз меньше массы атома водорода.
Позже Рентген (1895 г.), изучая катодные лучи, нашел новый вид излучения — Х-лучи (или рентгеновские лучи ), которые имеют большую проникающую способность и вызывают флюоресценцию различных веществ. Еще одним важным событием стало открытие Беккерелем явления радиоактивности и опыты Кюри и Склодовской-Кюри, которые установили, что соли урана и тория излучают особые лучи, которые вызывают почернение фотопластинок. Следствием их работы было открытие двух новых элементов — полония и радия.
Радиоактивность — это способность атомов некоторых элементов самопроизвольно излучать невидимое глазу лучи, которые вызывают почернение фотопластинок, проходят через вещества и ионизируют воздух.
Экспериментальные доказательства сложности природы атома поставили ученых перед необходимостью создать новую теорию — так называемую модель атома . Наиболее известными стали первые модели строения атома, разработанные У.Томсоном-Кельвином (1902г.), Х.Нагаокой (1904г.), Дж.Томсоном (1904г.), Ленардом (1904г.). Однако предложенные модели атома были, главным образом, гипотетическими и качественными, то есть не подтверждались суровыми математическими выкладками. И только Резерфорд опирался на точные экспериментальные данные и расчеты.
Результатом многочисленных экспериментов стала планетарная модель строения атома Резерфорда (1911г.), которая базируется на таких утверждениях:
- атом — электронейтральна система, состоящая из ядра и электронной оболочки;
- в центре атома находится положительно заряженное ядро, радиус которого (~ 10-15 м) составляет мизерную часть радиуса атома (~ 10-10 м)
- все положительный заряд и почти вся масса атома сосредоточены в его ядре;
- вокруг ядра вращаются электроны, количество которых равно положительному заряду ядра.
Опыты Резерфорда позволили установить фундаментальную зависимость, ныне известную как закон Мозли :
Заряд ядра атома численно равен порядковому номеру элемента в периодической системе Д.И.Менделеева.
Ядерная модель Резерфорда подтверждалась большим количеством экспериментальных данных и была значительным шагом вперед в процессе познания строения атома. Однако она не способна была объяснить некоторые известные факты и имела определенные недостатки. Главным из них была невозможность аргументировать устойчивость атомов. Второй существенный недостаток теории Резерфорда — невозможность на ее основе объяснить происхождение линейчатых спектров, поскольку при непрерывном излучении энергии электроном, как следовало из модели Резерфорда, атомные спектры должны быть сплошными, но в действительности они линейчатые.
На основе модели Резерфорда, квантовой теории света, линейчатой природы спектров, открытие дискретных свойств электрона в атоме Бор предложил новую теорию (1913г.), согласно которой электрон трактовался как материальная частица, которая имеет определенные массу и заряд и движется исключительно по круговым стационарным траекториям — так называемым «разрешенным орбитам». Такое предположение следует в первую очередь из анализа атомных спектров — их линейчатый характер свидетельствует о дискретности (прерывистость) значений внутренней энергии атома.
Атом не способен непрерывно менять свое энергетическое состояние, монотонно поглощая или излучая энергию (иначе атомные спектры были бы сплошными). Атом, который находится в определенном ( основном ) состоянии с определенным запасом энергии Е1 при поглощении новой порции энергии переходит в другое ( возбужденное ) состояние Е2 , но через некоторое время для возвращения своего основного состояния он должен отдать поглощенную ранее энергию.
Основные положения теории строения атома Бор сформулировал в виде двух постулатов.
Первый постулат Бора :
Электрон, не излучая и не поглощая энергии, вращается вокруг ядра только на определенных круговых орбитах, которые называются стационарными, или квантовыми.
Радиус стационарной орбиты r и скорость электрона на ней υ связанные квантовым соотношением Бора
- mυ=nh2π, где m — масса электрона; n — номер орбиты; h — постоянная Планка (h = 6,626 · 10 — 34 Дж · с).
Бор установил, что радиусы орбит соотносятся как квадраты небольших целых чисел, равны номерам орбит:
r 1 : r 2 : r 3 …: r n = 1 2 2 2 3 2 …: n 2 ,
а скорости электронов на квантовых орбитах — обратно пропорциональны номерам орбит:
υ 1 : υ 2 : υ 3 … υ n ~ 1/1: 1/2: 1/3 … 1 / n …
Второй постулат Бора :
Электрон может переходить с одной стационарной орбиты на другую, при этом поглощается или излучается квант электромагнитного излучения, энергия которого равна разности энергии атома в конечном и исходном состояниях.
Из постулатов Бора следует, что атомы существуют, не изменяя своей энергии, только в определенных стационарных состояниях, которые образуют дискретный ряд энергий Е 1 , Е 2 , …, Е n , причем при поглощении или излучении энергии атом скачкообразно переходит из одного состояния в другой.
Энергия электрона, вращающегося вокруг ядра, зависит от радиуса орбиты. Наименьшую энергию электрон имеет ближайшей к ядру орбите. Состояние, соответствующее наименьшему запасу энергии атома, называется основным . Чтобы перевести электрон на более удаленную от ядра орбиту, необходимо преодолеть его притяжение к положительно заряженному ядру, что требует затраты энергии. Этот процесс осуществляется благодаря поглощению кванта энергии. Энергия атома при таком переходе увеличивается, и он переходит в возбужденное состояние. Возвращение электрона в исходное состояние приводит к уменьшению энергии атома, поскольку она выделяется в виде кванта электромагнитного излучения.
Энергия кванта, излучаемого электроном при переходе, равна
- E=E2-E1, где E1 и E2 — соответственно энергия электрона в основном состоянии и на более удаленной от ядра орбите.
Бор установил зависимость, которая позволяет вычислить возможные частоты ν излучения, которое поглощает или излучает атом, то есть вычислить спектры атомов:
- ν=E2-E1h
Теория Бора о строении атома водорода была достаточно наглядной и удобной. Она показала сложность строения атома, наличие стационарных состояний, при которых не происходит излучение энергии, объяснила дискретную природу атомных спектров как следствие перехода электронов с одной орбиты на другую и обосновала возможность существования неизвестных в то время спектральных серий атома водорода в ультрафиолетовой и инфракрасной областях спектра. И самое главное — теория Бора наглядно доказала невозможность применения законов классической физики к изучению строения атома и тем самым дала мощный толчок к развитию квантовой физики.
Но наряду с успехами у теории Бора были и внутренние противоречия. Так, с одной стороны, по Бору электрон в атоме не подлежит законам классической физики, а с другой — эти законы использовались для расчета сил, действующих на электрон в атоме.
Теория Бора ограничивалась объяснением строения атома водорода — одноэлектронной системы, в которой действуют только кулоновские силы. Однако она не могла быть использована для расчета многоэлектронных систем, в которых, кроме кулоновских сил притяжения, действуют и электростатические силы отталкивания между электронами.
Теория Бора не смогла также осветить мультиплетность спектральных линий и их различную интенсивность. Были выяснены и некоторые вопросы, связанные с постулатами. Например, переход электрона с одной стационарной орбиты на другую происходит в течение определенного времени. При этом электрон находится в промежуточном состоянии между конечной и начальной орбитами, но такое положение запрещается самой теорией Бора.
Однако несмотря на определенные недостатки, теория Бора стала поворотным этапом в развитии современных представлений о строении атома.
Квантовая теория строения атома
Первые модели показали, что нельзя автоматически распространять законы природы, справедливые для больших тел — объектов макромира, на малые объекты микромира. Поэтому и возникла необходимость в разработке новой физической теории для описания свойств и поведения объектов микромира. Этой теорией стала квантовая или волновая механика , которая основывается на таких принципах :
- квантования энергии Планка;
- двойственности свойств, или корпускулярно-волнового дуализма электрона (уравнение Де Бройля)
- неопределенности Гейзенберга;
- волнового характера движения электрона (уравнение Шредингера).
При изучении особенностей спектров Планк (в 1900 г.) ввел некоторые предположения. Во-первых, фотон является неделимым и существует в виде дискретного образования. Во-вторых, лучистая энергия излучается и поглощается не непрерывно, а дискретно, то есть небольшими порциями (квантами), энергия которых зависит от частоты ν согласно уравнению Планка:
- E=h⋅ν
Предположение Планка блестяще подтвердились после открытия фотоэффекта, который доказывает, что фотон является носителем корпускулярных свойств ( корпускула — частица), а его волновая природа проявляется в явлениях дифракции и интерференции света. Итак, фотон является одновременно и частицей, и волной, то есть имеет двойственные свойства (такой признак микрообъектов называется корпускулярно-волновым дуализмом). Но от обычной частицы электрон отличается невозможностью точно определить его положение, поскольку невозможно точно определить положение волны, а от волны — невозможностью делиться на доли.
Волновые свойства фотона выражаются через связь длины волны λ его электромагнитного колебания с частотой ν и скоростью распространения c:
- λ ⋅ ν= cλ⋅ν=c
Из этих уравнений следует соотношение, связывающее корпускулярную характеристику фотона Е с волновой λ:
- E=hc/λ
Однако фотон с энергией Е имеет и некоторую массу m согласно уравнениям Эйнштейна (1905г.):
- E = mc2
Из сравнения уравнений следует mc2=hc/λ, откуда
- λ = hmc
Произведение массы на скорость называется количеством движения, или импульсом и сказывается р = m · c . Поэтому
- λ = hp
Эти уравнения сочетают как волновые, так и корпускулярные свойства фотона.
Развивая это положение, Де Бройль (1924 г.) впервые высказал гипотезу, что корпускулярно-волновой дуализм проявляют не только фотоны, но и электроны, поэтому для них должны выполняться аналогичные соотношения, которые показывают, что для электрона с массой m и скоростью υ длина волны, которую принято называть волной Де Бройля , равна:
- λ = hmυ
Эта зависимость называется уравнением Де Бройля и характеризует двойственную, корпускулярно-волновую природу электрона в атоме.
Согласно гипотезе Де Бройля корпускулярно-волновой дуализм (двойственная природа) электрона доказывается наличием одновременно как свойства частицы (корпускулы), имеющий некоторую массу m и скорость υ , так и свойствами волны с определенной длиной волны λ и частотой колебаний ν. Волновые свойства электрона экспериментально подтвердились в опытах по их рассеивании и дифракции (1927 г.), а в настоящее время они широко применяются в научных методах при исследовании строения вещества, например, в электронографии.
Сравнение волновых (λ) И корпускулярных (m) свойств электрона
- λ : mλ:m= 0,332 · 10 -9 · 9,1095 · 10 -31 ~ 3,7 · 10 20
свидетельствует о значительном (~ 20 порядков) преимущество волновых свойств электрона над корпускулярными. На этом базируется принцип неопределенности Гейзенберга (1927 г.):
невозможно однозначно и точно установить скорость электрона и его координаты.
Математическое выражение принципа неопределенности имеет вид
- Δ x Δ p ≥ h2 или Δ x Δ υ ≥ h2πm, где Δ x , Δ p , Δ υ — соответственно неопределенности в координате, импульсе и скорости электрона.
Из этой формулы следует: чем точнее определена координата электрона (то есть чем меньше погрешность в определении координаты Δx), Тем менее определенной становится величина импульса (то есть погрешность в определении импульса стремится к бесконечности) и наоборот: чем точнее определенный импульс (скорость), тем более неопределенное местонахождение электрона . Так, если при радиусе атома примерно 10-10 м положение электрона определено с точностью всего до 10-12 м, то неопределенность в скорости будет составлять 58000000 м / с (при скорости электрона 2,187 · 106 м / с).
Итак, квантовая механика отказалась от уточнения местонахождения электрона, а заменила классическое понятие точных координат понятием статистической вероятности его нахождения в данном элементе объема dV вокруг ядра.
Поскольку положение электрона в атоме неопределенное, можно говорить лишь о вероятности его пребывания в той или иной точке атомного пространства, которую определяют с помощью волнового уравнения Шредингера (1925 г.), что связывает потенциальную U и полную Е энергии электрона с волновой функцией «пси» ψ, которая в определенной степени аналогична амплитуде трехмерного волнового процесса. Для одноэлектронного атома водорода уравнения Шредингера имеет вид:
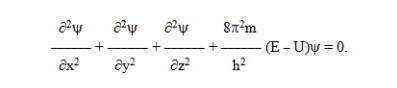
Допустимыми решениями уравнения Шредингера являются функции ψ1, ψ2, ψ3, . . . , ψn, каждой из которых соответствует свое значение энергии Е1 , Е2 , Е3 , … Э n . Волновая функция не имеет строгого физического содержания, она только уподобляется трехмерной амплитуде колебания, но не идентична ей. Однако физический смысл имеет произведение ψ2dV, характеризующее вероятность локализации электрона в элементарном объеме околоядерного пространства dV = dxdydz .
На волновую функцию накладываются граничные условия , или требования регулярности — ограничения, которые определяют область существования функции. Согласно правилу граничных условий ψ должна быть:
- непрерывной , так как состояние квантовой системы меняется непрерывно;
- конечной , то есть она не должна превращаться в ∞ ни при каких значениях аргумента;
- однозначной , поскольку функция ψ, которая является аналогией амплитуды вероятности, должна иметь единственное значение в любой точке пространства;
- предельной , то есть превращаться в ноль при бесконечно большом удалении от ядра;
- нормированной — это значит, что суммарная вероятность нахождения электрона в околоядерном пространстве должна быть равна единице; математически условие нормирования записывают так: ∫ψ2dV= 1.
Подобно амплитуды любого другого процесса волновая функция может принимать как положительных, так и отрицательных значений. Однако величина ψ2 всегда положительная. При этом она удивительным свойством: чем больше значение ψ2 в какой-то точке пространства, тем выше вероятность того, что электрон обнаружит там свое действие, то есть его существование может быть открытым в физическом процессе.
Волновая функция ψ, которая является решением уравнения Шредингера, называется орбиталью.
Итак, орбиталь — это математическое понятие, но часто пользуются и упрощенным толкованием:
Орбиталь — это пространство вокруг ядра, в котором вероятнее всего пребывания электрона.
Наряду с понятием орбиталь в квантовой механике применяется представление о электронном облаке — модели состояния электрона в атоме, плотность соответствующих участков которой пропорциональна вероятности пребывания там электрона . То есть максимальная плотность электронного облака пропорциональна квадрату волновой функции ψ2. Одна из возможных форм электронного облака показана на рисунке. Очевидно, чем крепче связь электрона с ядром, тем электронное облако меньше по размеру и компактнее распределением энергии.
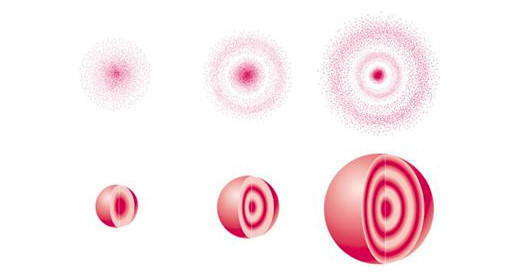
Атомные орбитали
Согласно квантово-механической теории атомную орбиталь и состояние электрона в атоме можно однозначно описать с помощью набора четырех квантовых чисел — энергетических характеристик состояния электрона в атоме . Три из них ( n— главное , l — орбитальное, m — магнитное) непосредственно вытекают из уравнения Шредингера, описывающее электрон как волну в трех координатах. Поэтому для полной характеристики энергетического состояния электрона в атоме нужны три целых числа. А четвертое квантовое число ( s — спиновое) характеризует некоторые особые магнитные свойства электрона.
Главное квантовое число n. По условиям квантования электрон в атоме может находиться только в определенных квантовых состояниях, соответствующих определенным значением его энергии связи с ядром. Переход электрона с одной квантового состояния в другое связан с скачкообразным изменением энергии. Итак, основной характеристикой электрона, вращающегося вокруг ядра, является его энергия.
Главное квантовое n определяет общую энергию электрона в определенном квантовом состоянии и характеризует радиус квантового уровня, то есть среднее расстояние от ядра к участку повышенной электронной плотности.
Для атома в нормальном (основном) состоянии главное квантовое число n приобретает все целочисленных значений от 1 до 7. Для атома в возбужденном состоянии n может принимать значения от 1 до бесконечности.
Состояние электрона, который характеризуется определенным значением главного квантового числа, называется энергетическим уровнем электрона в атоме. Для обозначения энергетических уровней, соответствующих разным значениям n , иногда используют латинские буквы (табл. 1.1). Понятно, что значение главного квантового числа n = 1 соответствует первому, ближайшем к ядру, энергетическому уровню, n = 2 — второй, значение n = ∞ указывает на полное удаление электрона из атома.
Таблица 1.1 — Обозначение энергетических уровней в атоме
| Главное квантовое число n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Обозначения энергетического уровня | K | L | M | N | O | P | Q |
Наименьшую энергию электрон имеет при n = 1; с ростом n энергия электрона увеличивается. При n = ∞ предполагают, что электрон имеет энергию, достаточную для его полного отделения от ядра (ионизация атома).
Главное квантовое число определяет и размеры электронного облака. Квантовые переходы электрона в атоме отвечают скачкообразном изменении среднего размера электронного облака: уменьшение энергии связи электрона с ядром вызывает увеличение объема облака и наоборот.
Орбитальное квантовое число l . Электроны, которые находятся на одном и том же энергетическом уровне, могут отличаться друг от друга по энергии связи с ядром, потому что они экранируются от ядра теми электронами, которые размещаются ближайшее от ядра. Итак, основные энергетические уровни состоят из некоторого числа энергетических подуровней.
Орбитальное (азимутальное, побочное) квантовое число l, которое характеризует энергию электрона на энергетическом подуровне и определяет форму электронного облака.
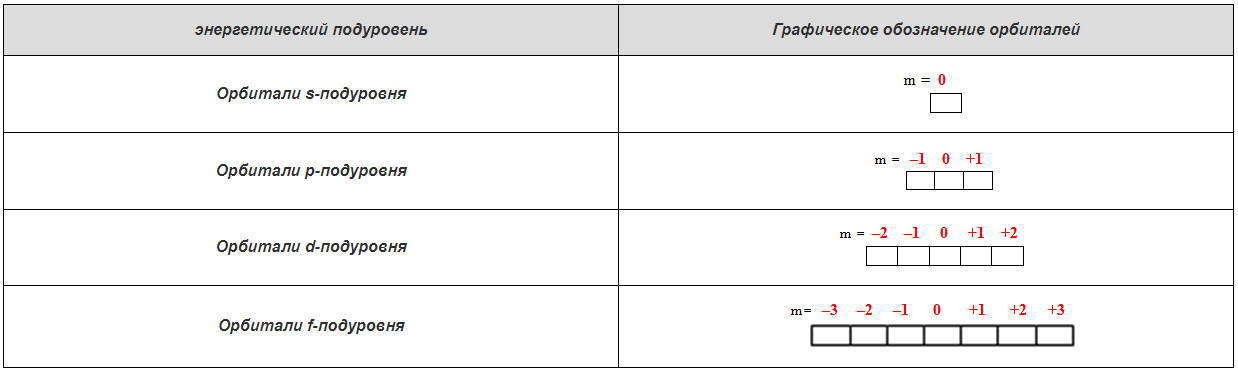
Орбитальное квантовое число может принимать n целочисленных значений от 0 до (n-1). Каждому значению l соответствует определенный подуровень, который обозначается латинской буквой s, p, d, f и т.д. (табл 1.2).
Таблица 1.2 — Обозначение энергетических подуровней
| Орбитальное (побочное) квантовое число l | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Обозначение энергетического подуровня | s | p | d | f | g | h |
Для определенного значения главного квантового числа n орбитальное квантовое число l может иметь n значений, то есть количество подуровней на любом энергетическом уровне равно номеру этого уровня . Например, на пятом энергетическом уровне (n = 5) орбитальное квантовое число может принимать пять значений от 0 до (5-1 = 4), то есть до (n-1). Итак, на пятом энергетическом уровне находится пять подуровней, каждый из которых имеет свое обозначение: 5s ( l = 0), 5p ( l = 1), 5d ( l = 2), 5f ( l = 3) и 5g ( l = 4). Значение главного n и орбитального lквантовых чисел для первых четырех энергетических уровней приведены в табл. 2.3.
Таблица 2.3 — Значение главного и орбитального квантовых чисел для четырех энергетических уровней
| Главное квантовое число n (номер энергетического уровня) | орбитальное квантовоечисло l | Обозначения энергетических подуровней |
|---|---|---|
| 1 | 0 | 1s |
| 2 | 0, 1 | 2s 2p |
| 3 | 0, 1, 2 | 3s 3p 3d |
| 4 | 0, 1, 2, 3 | 4s 4p 4d 4f |
Согласно буквенных обозначений энергетических подуровней электроны, находящиеся на них, называются s-, p-, d-, f- электронами , причем для каждого энергетического уровня n наименьшую энергию имеют s-электроны, затем р-, d- и f-электроны.
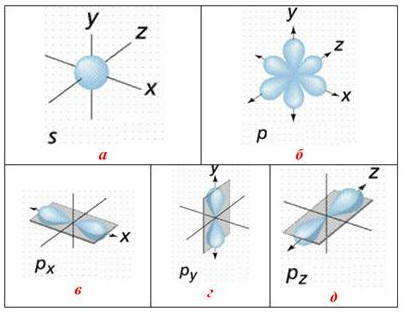
Квантово-механические расчеты определяют форму орбиталей: s-орбитали имеют форму шара (сферическая симметрия), p-орбитали — гантели, d-орбитали — лепестковую форму, а f-орбитали — более сложную форму.
Состояние электрона в атоме, соответствует определенным значением n и l , записывают так: сначала цифрой обозначают главное квантовое число, а затем буквой — орбитальное. Например, запись 3р обозначает электрон, который характеризуется главным квантовым числом n = 3 (находится на третьем энергетическом уровне) и орбитальным квантовым числом l = 1 (орбиталь имеет форму гантели).
Магнитное квантовое число m. Из уравнения Шредингера следует, что ориентация орбитали в атоме не может быть произвольной, поскольку движение электрона вокруг ядра вызывает появление магнитного поля. Поэтому состояние электрона зависит от его орбитального магнитного момента.
Магнитное квантовое число m характеризует энергию электрона на орбитали и определяет пространственное размещение орбитали относительно магнитного поля, то есть величину проекции орбитального момента количества движения на направление магнитного поля.
Магнитное квантовое число может принимать следующие значения: 0, ± 1, ± 2, … ± l . Число значений зависит от орбитального квантового числа l и равна (2 l 1) (табл. 1.4).
Таблица 1.4 — Количество орбиталей на энергетическом подуровне в зависимости от значений орбитального и магнитного квантовых чисел
| Орбитальное квантовое число l и обозначения подуровня | Магнитное квантовое число m | Количество орбиталей на энергетическом подуровне при данном значении l |
|---|---|---|
| l = 0 (s- подуровень ) | 0 | 1 |
| l = 1 (p- подуровень ) | -1, 0, +1 | 3 |
| l = 2 (d- подуровень ) | 2, -1, 0, +1, +2 | 5 |
| l = 3 (f- подуровень ) | -3, -2, -1, 0, +1, +2, +3 | 7 |
Орбитали с одинаковой энергией называются вырожденными. Поэтому можно сказать, что p-состояние вырожденно три раза, d-состояние — пять, а f-состояние-семь раз.
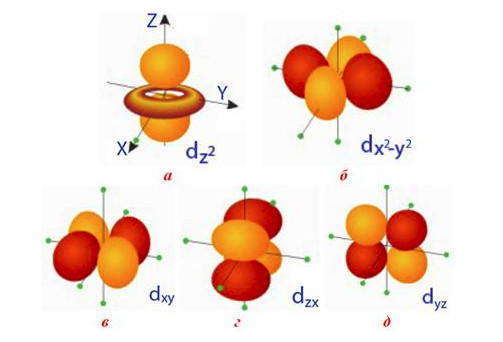
В отличие от шаровидной s-орбитали, р, d-, f-орбитали имеют определенную ориентацию в пространстве, по характеру которой р-орбитали обозначают р х р в р z (вытянутые вдоль осей х , в, z). Направление d-орбиталей не только совпадает с осями координат, но и лежит между ними: d-орбитали, ориентированные вдоль осей координат, обозначают d x 2 -d y 2 (вытянутые вдоль осей х и у) и d z 2 (вытянутые вдоль оси z) d-орбитали, ориентированные между осями координат, обозначают d xy , d yz , d xz (расположены на биссектрисам между осями координат).
Формы орбиталей: а) сферическая s-орбиталь, которая имеет наименьшую энергию и размещается ближе к ядру по сравнению с другими орбиталями данного энергетического уровня; б) три р-орбитали: чем выше энергия р-электрона, тем скорее он вращается вокруг ядра и тем сильнее вытягивается область его существования, образуя гантелеподобную форму; в) p x орбиталь; г) p y орбиталь; д) p x орбиталь
Пять d-орбиталей с одинаковой энергией, но разной формы: четыре из них имеют лепестковую форму, а последняя — форму гантели, пропущенной сквозь кольцо. Направленность d-орбиталей может не только совпадать с осями координат, но и размещаться между ними: а) d-орбиталь, расположенную вдоль оси z, обозначают d z 2 ; б) d-орбиталь, ориентированные вдоль осей x и y, обозначают d x 2 -d y 2 ; в, г, д) три d-орбиталей, вытянутые между осями координат, обозначают d xy , d yz и d xz
Общий вид и обозначения f-орбиталей:
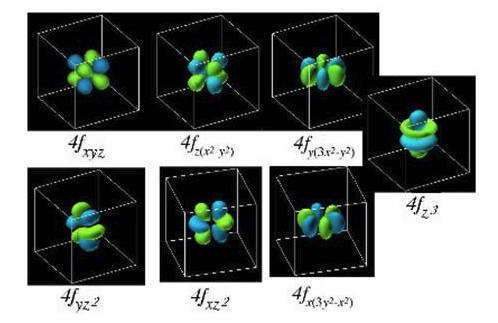
Таблица 1.5 — Графическое изображение орбиталей в виде квантовых ячеек, над которыми записаны соответствующие значения магнитного квантового числа m :
Спиновое квантовое число , или просто спин ms (однако на практике чаще пользуются сокращенным обозначением спинового квантового числа, оставляя только один символ — s ). Его название происходит от англ. spin — кручение, вращение. На основе изучения тонкой структуры атомных спектров установлено, что состояние электронов в атоме, кроме вращения вокруг ядра, которое определяется квантовыми числами n, l, m, Зависит от собственного движения — спина. Сначала для наглядности считали, что это явление аналогичное вращению Земли вокруг своей оси во время движения вокруг Солнца. В настоящее время мнения относительно физического смысла спинового квантового числа диаметрально противоположные во многих ученых, занимающихся квантовой химией. Одни доказывают, что спин — это чисто квантово-механическая признак электрона, не имеет классических аналогов, а только отражает наличие у электрона собственного момента количества движения. Другие уверены, что ms характеризует вращение электрона вокруг собственной оси по часовой стрелке или против нее, в зависимости от чего спиновом квантовому числу приписывают знак «+» или «-».
Гипотетическая модель спинового квантового числа, достоверно не доказана, но и доказательно не опровергнутая:
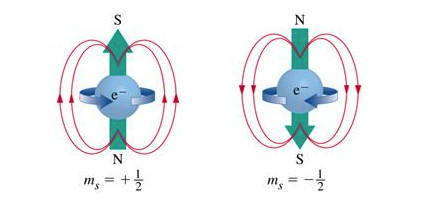
Спиновое квантовое число ( ms или s ) — это собственный момент импульса электрона, который не связан с его движением в пространстве.
Спиновое квантовое число может иметь только два значения: + ½ и -½. Спин изображают противоположно направленными стрелками:
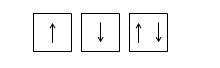
Спины электронов, направлены в одну сторону, называются параллельными , а в противоположные стороны — антипараллельными .
Последовательность заполнения электронами энергетических уровней
Состояние электронов в атоме можно однозначно описать с помощью четырех квантовых чисел n, l , m, s. Однако для исчерпывающего объяснения строения электронных оболочек необходимо знать три фундаментальных положения.
Принцип Паули
Принцип Паули (1925 г.) позволяет определить такие комбинации квантовых чисел, которые соответствуют реальному распределения электронов в атоме. Принцип Паули , который иногда называют запретом Паули , формулируется так:
В атоме не может быть двух или более электронов с одинаковыми значениями всех четырех квантовых чисел.
Иначе говоря, каждый электрон имеет собственный набор четырех квантовых чисел. Из этого следует несколько последствий.
Первое следствие принципа Паули :
Одну орбиталь, характеризующаяся определенными значениями квантовых чисел n, l, m, могут занимать не более двух электронов с антипараллельными спинами.
Например, на первом энергетическом уровне (n = 1) и орбитальное квантовое число и магнитное квантовое число могут иметь только одно значение: l = 0 (что указывает на s-подуровень) и m = 0 (что указывает на сферическую форму орбитали). На этой единой орбитали 1s-подуровня размещаются только два электрона, для которых совпадают квантовые числа n, l , m, но отличаются значение спинового квантового числа s, а именно:
1 электрон: n = 1, l = 0, m = 0, s = +1/2;
2 электрон: n = 1, l = 0, m = 0, s = -1/2.
Второе следствие принципа Паули :
максимальное количество электронов на энергетическом подуровне, характеризующееся квантовыми числами n и l , равна 2 (2l + 1).
Итак, на s-подуровне ( l = 0) может максимально находиться 2 (2 · 0 + 1) = 2 электрона, на р-подуровне ( l = 1) 2 (2 · 1 + 1) = 6, на d- подуровни ( l = 2) — 2 (2 * 2 + 1) = 10 на f- подуровне ( l = 3) — 2 (2 * 3 + 1) = 14 электронов.
Третье следствие принципа Паули :
максимальное количество электронов на любом энергетическом уровне, характеризующееся главным квантовым числом n , равна 2n2 .
Исходя из этого, легко рассчитать возможное количество электронов на любом энергетическом уровне: на первом (n = 1) может находиться 2 · 12 = 2 электрона, на втором (n = 2) — 2 * 22 = 8, на третьем (n = 3) — 2 * 32 = 18, на четвертом (n = 4) — 2 · 42 = 32 электроны.
Таким образом, принцип Паули определяет максимальную емкость уровней, подуровней и орбиталей.
Принцип минимума энергии
Стойким является такое состояние атома, в котором электроны находятся в низких энергетических уровнях. согласно принципу минимума энергии:
В атоме электроны заполняют свободные орбитали с минимальными энергиями, соответствует их прочном связи с ядром.
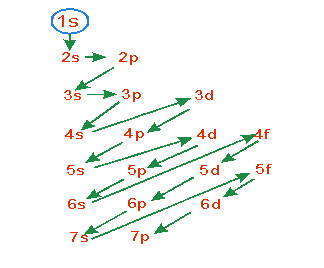
Поскольку энергия электрона определяется квантовыми числами n и l , то последовательность заполнения атомных орбиталей зависит от значений этих квантовых чисел, как установил В.М.Клечковський (1961г.).
Первое правило Клечковского :
При увеличении заряда ядра атома последовательное заполнение электронных орбиталей происходит от орбиталей с меньшим значением суммы главного и орбитального квантовых чисел (n + l) к орбиталей с большим значением этой суммы.
Второе правило Клечковского :
При одинаковых значениях суммы (n + l) заполнение орбиталей происходит последовательно в направлении роста главного квантового числа n.
Например определим последовательность заполнения подуровней 2s, 2p i 3s. Для них суммы главного и орбитального квантовых чисел равны:
2s: n + l = 2 + 0 = 2;
2p: n + l = 2 + 1 = 3;
3s: n + l = 3 + 0 = 3.
Согласно первому правилу Клечковского сначала заполняется 2s-подуровень, для которого сумма n + l меньше, за ним 2р-подуровень, а затем 3s, который хотя и имеет такую же сумму n + l, что и 2р, но характеризуется большим значением главного квантового числа.
По мере роста энергии орбиталей соответствующие подуровни образуют последовательность — так называемую шкалу энергии :1s<2s<2p<3s<3p<4s<3d<4p<5s<4d<5p<6s≈4f≈5d<6p<7s≈5f≈6d<7p1s<2s<2p<3s<3p<4s<3d<4p<5s<4d<5p<6s≈4f≈5d<6p<7s≈5f≈6d<7p
Если энергии близких подуровней (таких, как 4f i 5d, 4s i 3d) очень мало отличаются между собой, то порядок заполнения подуровней усложняется, и электроны могут находиться то на одном из них, то на другом.
Согласно приведенной схемы меняется и энергия электронов. На каждом следующем уровне энергия электронов больше, чем на предыдущем, а связь с ядром соответственно меньше. В пределах определенного энергетического уровня энергия электронов увеличивается при переходе с s-подуровня на р и с р на d-подуровень.
Правило Гунда
В пределах одного подуровня последовательность заполнения орбиталей тоже не является произвольной, она определяется правилом Гунда :
Устойчивому состоянию атома соответствует такое распределение электронов на энергетическом подуровне, при котором абсолютное значение суммарного спинового числа является максимальным.
Иными словами, электроны определенного подуровня занимают максимально возможное количество вырожденных орбиталей, то есть на смежных орбиталях одного подуровня сначала размещаются электроны с параллельными спинами, а затем те же орбитали заполняются электронами с антипараллельными спинами. При другом размещении электронов абсолютное значение суммарного спина НЕ будет максимальным. Так, если атом имеет d-подуровня пять электронов, то они размещаются по схеме
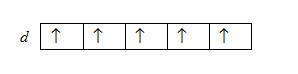
Правило Гунда не запрещает иного распределения электронов в пределах подуровня. Оно лишь утверждает, что максимальное значение суммарного спина соответствует устойчивому (невозбужденном) состояния, в котором атом имеет наименьшую возможную энергию. При любом другом распределении электронов энергия атома будет больше, следовательно, атом будет находиться в возбужденном неустойчивом состоянии.

Давным давно, в школе и инсиитуте, я (мне 61 год) изучал ядерную физику.
Изучал без особых успехов — на 3 — чку.
Прошло много лет и стали появляться вопросики, как будто сами собой:
1. Почему в атоме равное количество электронов, нейтронов, протонов?
2. Почему в электроне и протоне равное количество кварков?
3. Почему протон и нейтрон находятся в ядрах неподвижно, но ведь у элементарных частиц нет массы покоя.
На все три вопроса удовлетворяет один ответ: одним выстрелом трех зайцев (может быть зайцев и побоььше, незнаю)
Объясняю на уровне табуретки (по другому не умею, знаний не хватает)
— Электрон, протон, нейтрон — это видоизмененные энергетические состояния одной частицы.
Одна частица — художник «рисует» нам и электрон и протон, и нейтрон на любом энергетическом уровне (орбитали).
Тогда:
1. Вот и получается равное количество электронов, протонов, нейтронов.
2. Если частица — художник одна, то почему у нарисованных ею электрона и протона должно быть разное количество кварков.
3. Когда частица — художник проходит через центр, она просто фиксирует состояние нейтрона и протона, не прекращая движения.
Выходит нейтрон и протон все таки движутся.
Скажу за траекторию 3-х мерное, компактно — замкнутое математическое многообразие Пуанкаре. Лучше не скажешь… хотя…
Кого рассмешил посмейтесь, кого удивил — удивляйтесь, кого разозлил — злитесь, но не сильно.
Алексей Артамонов. Точильщик маникюрного и парикмахерского инструмента. Г. Самара.
23 мая 2021 г.
Мне 65 лет. школьную физику хорошо помню. Сейчас заинтересовался физикой микромира.
Два вопроса:
1. S-орбиталь — сфера, ядро атома в центре, понятно. Р- орбиталь — лепестковая форма,
в каком месте находится ядро атома, если вокруг него вращаются электроны?
2. Спин электрона — наклон оси вращения как соотносить — к плоскости орбиты?
Сергей. Радиоинженер.